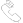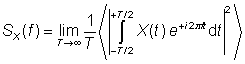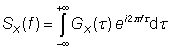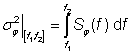当采用光谱分析仪来测量一些激光光源的光功率谱分布情况时,结果通常是功率谱密度(单位为 mW/nm或者 dBm/nm,其中dBm是分贝毫瓦,是相对于1mW的分贝值)或者给定测量带宽的功率。
考虑功率谱密度时,有许多相关的量。主要考虑两个问题:
任何情况下,都存在处于某些波长或者频率范围的能量、功率和强度等。相应的,积分量具有的单位分别为焦耳、瓦特和瓦特每平方厘米等。
光功率谱密度可以是单位频率间隔(THz)的光功率,也可以是单位波长间隔(nm)的光功率。如果积分量的单位为瓦特,得到的功率密度为 W/THz或者 W/nm。它们之间转化时需要注意,因为转化因子与波长相关,频率和时间间隔为极小量时,应该根据 dν = (c / λ2) dλ进行转化。这表明波长越短时,每nm对应更多的THz。这导致的结果是光谱的峰值位置与功率谱密度采用频率间隔或波长间隔有关。如果忽视这一问题就会出现混淆或者得到的功率谱密度有错误。参看图1和图2。
图1:不同温度黑体的功率谱密度,由普朗克定律得到,功率谱密度采用频率间隔表示。
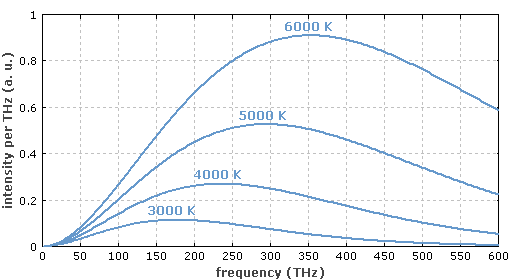
图2:与图1相同,功率谱密度采用波长间隔表示。这样改变了峰值位置。例如温度为6000K时,峰值为483nm,对应的频率为621 THz,而在上图中该温度下的峰值为353 THz.
需要采用光功率谱密度给出脉冲形状光谱图。在这种情况下,功率谱密度是从一些窗口方程中提取一些数据在有限时间内进行傅里叶变换得到。
噪声功率谱密度
噪声PSD是指单位噪声频率(而不是光学频率)的平均功率。这一噪声PSD存在于几乎任何光学或者电子信号中。可以结合光功率一起使用,也会与相位噪声,频率噪声,脉冲时间噪声,脉冲能量或锁模激光器中的时间抖动一起讨论。类似的,PSD适用于电压或者电流中。
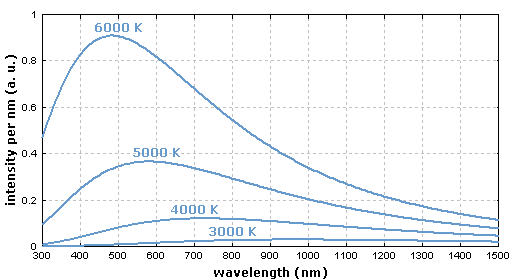
图3:固体激光器的强度噪声光谱。这里显示的是功率谱密度相对于散粒噪声的曲线。
PSDs可以定义为关注量傅里叶变换的模平方,但是这一直接方法仅仅当有限时间间隔内方程不为0 的情况。而常见的情形是方程在某一个平均值附近涨落(例如,考虑激光器功率或者相位涨落时),定义为:
可以适用于X(t)变化情况时的PSD。这里,积分限制在一个有限时间间隔(因此得到的积分值是收敛的),傅里叶变换的模平方需要除以时间间隔T。最后计算当时间间隔T很长时的结果。这一定义意义非常清晰,但有时不方便(尤其是解析计算时)。因此可以采用Wiener-Khinchin理论,即
其中
是X(t)的自相关函数。
在任何情况下,功率谱密度都是统计测量结果,可以对测量得到的真实数据取平均估计其值。简单测量一个轨迹只能得到粗略的PSD。
功率谱密度可以表示为单边方程,即频率只取大于0的值,或者表示为两边方程,频率可正可负。通常采用光谱分析仪得到的光功率密度是单边的。工程理论中的噪声PSDs也都是单边的,而在物理理论中则是双边的。噪声功率密度由电子光谱分析仪测量,然后计算在时间域得到的数据。相对强度噪声表示为 dBc/Hz(相对于带宽为1 Hz的载流子的dB值),或者表示相位噪声为rad2/Hz。有时需要指明功率密度的平方根,单位为rad/√Hz。
在一定噪声频率范围内的关注量(例如,光相位)的方差由PSD的积分得到:
其平方根等于均方根值。然而,这一积分不总是收敛(例如,当PSD存在f=0的奇点时)。而相位噪声中,发散对应的是有限线宽。噪声积分用于计算信噪比。
然而,测量或者计算功率谱密度容易出现很多错误。一些常见错误为:
混淆单边或者双边PSDs,或者没有弄清楚采用哪种
电子光谱分析仪设置错误,例如,考虑探测器模式和平均方法
没有在电子光谱分析仪得到的数据中添加纠正因子(例如,有效噪声带宽)
当由时间域的数据计算PSDs时没有选择合适的窗口消除错误
在实验环境中正确处理功率谱密度需要在数学基础,物理原理和电子光谱分析仪方面进行充足的培训。