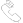菲涅尔数最初在衍射理论中提出来是用来描述光束传播的。如果光先通过大小为a的孔而后传播距离L后到达屏幕，这是采用菲涅尔数表达式为： 

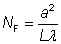
其中 λ 是波长。 

当菲涅尔数小于1时，发生夫琅禾费衍射，屏幕上显示的为孔的远场衍射图像，与光场通过孔径后空间复振幅分布的傅里叶变换相关。 

菲涅尔数等于或者大于1表示发生的是菲涅尔衍射（或者近场衍射），这时数学表示非常复杂。当菲涅尔数和衍射角度不大时，可以采用菲涅尔近似。 

共振腔的菲涅尔数 

菲涅尔数在光学谐振腔（腔）中也有重要作用，尤其是激光器谐振腔中。同样采用方程： 

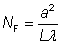
这里a是端反射镜的半径，L为谐振腔长度。 

具有比较大的菲涅尔数（大于1）的谐振腔表明对于普通的模式大小（即不在谐振腔的稳定限度，该处模式大小会变化），端反射镜的衍射损耗很小。这在稳定的激光器谐振腔中是正常的情况。相反的，如果菲涅尔数比较小，衍射损耗会很大，尤其是对于高阶模式，因此最好采用衍射极限工作。 

许多稳定的激光器谐振腔具有相对较大的菲涅尔数，不稳定谐振腔中的菲涅尔数较小，这通常用于高功率激光器。 

在分析法布里珀罗干涉仪的模式时，菲涅尔数也是一个很重要的参数。