参量放大是一种信号光可以利用参量非线性和泵浦光放大的现象。此词条针对于光学参量放大，并不包括针对微波的电学参量放大。对于光学参量放大器，可以利用某些非线性晶体材料的 χ(2)非线性或者利用光纤中的χ(3)非线性。 

参量放大的物理机制是基于光学非线性的。它与通过被激发原子或离子的受激辐射的产生的激光放大不同。参量放大并不会将介质激发到更高的能量水平（虽然在一些常用的解释中会涉及一些虚拟的激发态）。还需要注意的是需要将简并和与非简并参量放大区分开来，因为它们具有相差很大的特点。 

简并参量放大 

在这里，我们考虑基于χ(2)非线性的参量放大。 

在非简的情况下，三个不同的光波之间发生相互作用，其角频率分别为 ω1，ω2和ω3。根据能量守恒，需满足ω3=ω1+ω2。泵浦光的频率为ω3，信号光为ω2，闲散光为ω1（交换ω2和ω1并不会对以下分析产生本质的改变）。对于平面波或准直的高斯光束，三个频率的光的复振幅记为A1，A2，A3，他们之间的关系可以由以下方程来描述： 

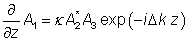
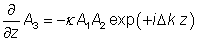
其中： 

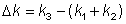
为以波数来计算的相位失配量，z是传播方向的坐标，并且κ是正比于材料非线性系数的耦合常数。如果将以上方程组中的复振幅由A3替换为iA3，则可以得到一个更对称的方程组。 

最简单的情况是没有相位失配的情况。当没有闲散光输入（即在晶体的首端A1= 0），则一开始没有信号放大，也没有任何泵浦损耗，但是会开始产生闲散光。如果最初的A3和A2是实的，则产生的闲散光也是实的。（该过程被称为差频产生）。接着会导A2的变大，即信号光的放大，以及泵浦光的损耗。 

将初始信号的相位旋转30°后再看这个过程会带来一些启发。此时，闲散光的相位会被旋转-30°。而信号光的被放大部分也被旋转了30°，因此信号光还是和以前一样被放大。这表明，在这种情况下放大是相位不敏感（即与信号相位不相关）。 

在另一种情况下，如果泵浦光相位被旋转30°。这也将会使得闲散光被旋转30°。两相变动相互抵消，从而不会改变信号光，因而信号光依旧被放大，并且只有闲散光的相位被改变。 

当存在相位失配（即非零的Δk）时，光波的相对相位将在传播期间发生变化，从而在一段距离之后，信号和闲散的功率会被反向转换回泵浦。因此，相位匹配对于有效的放大至关重要，且只在有限的频率范围内能实现。在某些特殊条件下，可以实现很大的相位匹配带宽。 

方程还表明，如果介质对闲散光有着显著的吸收的时候，由由于闲散光幅度小，因此信号光的放大也会被减小。因此，非线性晶体的透射范围必须足够大，从而对闲散波的损耗足够小，虽然很多应用对于闲散光本身并不感兴趣。然而，有一些情况下，对闲散光的一定程度的吸收可能是有利的。 

以上所使用的公式是根据经典物理学的。在量子力学中，在有些情况下泵浦光子被转换成信号-闲散光子对。使得信号和闲散光是强相关的，从而导致非经典光学特性。 

简并参量放大 

在简并参量放大中，信号光和闲散光在频率和偏振上都是相同的，也就是说，它们是无法区分的。有因此只有信号振幅A1和一个泵振幅A2，而没有闲散光。信号波长则恰好为泵浦波长的两倍。它们之间的相互作用利用以下方程描述： 

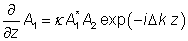
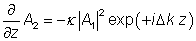
其中 

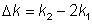
在这里，放大是相位敏感的。如果信号和泵浦的振幅是正实数，则信号被放大（对于零相位失配）。否则，如果泵浦光的符号被改变后则会产生信号光的衰减。能量转移的方向由A12 A2*的复相位决定。 

相位敏感的放大为压缩态光的产生提供了一种机制。并且在原则上它并不会产生额外的放大器噪声。然而，由于需要保持泵浦和信号之间的固定的相位关系，使得这种光放大在光纤通信中变得很不方便。 

光纤中的参量放大 

由于材料的中心对称性质，玻璃纤维不表现出χ(2)非线性（除非在某些情况下，例如，在强大的电场中被“极化”的光纤）。然而，参量放大，也可能由于χ(3)非线性导致。在这种情况下，会涉及四个不同的频率：两个泵浦频率，一个信号频率和一个闲散频率。一个常见的情况是部分退化的情况，即只有一个泵浦光频率。 

它们之间相互作用有点复杂，因为信号和闲散的光的相位会同时受到交叉相位调制（XPM）和光纤的色散的影响。（对于强的信号，还会有自相位调制的加成作用）。参量放大只会在泵浦波长的附近存在。当色散作用很弱时其范围可以是相当宽的，且其宽度依赖于泵浦功率。 

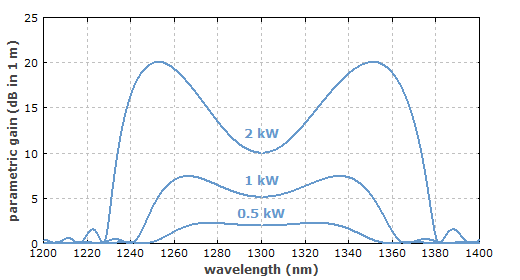
   图1 色散为−2000 fs2/m的1m光纤的参数增益谱随着泵浦光功率的变化。 

图1给出了一种情况下的参量增益谱。最高增益出现在XPM和色散效应相互抵消的使得相位匹配满足的波长。这只在反常色散下才会出现。 

参量增益主要在短脉冲传播下发生。利用数值模拟可以模拟这种过程，当然在这一过程中会有多种效应起作用。多模光纤中的相互作用是更为复杂的，因为不同传播模式之间的相位匹配更为复杂。