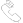激光增益介质(如稀土掺杂晶体或者光纤)中能级粒子数的动力学通常采用速率方程系统作为模型。这是一组微分方程,描述个能级粒子数在入射光导致的非辐射跃迁过程中随时间变化的情况:
吸收过程,包含激发态吸收
自发和受激辐射
多光子跃迁
能级转移从而引起上转换和淬灭效应
速率方程模型可以是一些更复杂的数值模型的一部分,描述光纤放大器或者体激光器中光功率的空间分布,或者调Q激光器的动力学行为。它们可以帮助我们理解激光器和放大器装置的工作过程,例如,去衡量一个装置的性能是否与基本原理决定的极限相近。
例子:掺铒增益介质的速率方程

图1:掺铒增益介质的能级和跃迁过程。
作为例子,这里考虑掺铒增益介质的动力学过程,它是被应用于掺铒光纤放大器中。图1给出了能级结构以及重要的辐射和非辐射跃迁。铒放大器和激光器工作在1500nm区域,是准三能级系统。为了简单起见,铒离子的能级以整数标在左边,例如,1代表基态4I15/2 ,2是上能态4I13/2。泵浦光为980nm,入射光束波长为1550nm时,发生光吸收和受激辐射跃迁,在图中用蓝色箭头代表,灰色箭头指自发辐射和非辐射跃迁。下面的跃迁过程 (2 → 1 )主要由自发辐射引起,而上面的跃迁(3 → 2 )是多光子跃迁占主导地位。只考虑下面三个能级之间的跃迁,假设激发态吸收跃迁至更高能级以及上转换过程都很微弱。
在这种情况下,速率方程可表示为:

这里 nj 代表j能级的粒子数百分比。例如,当所有离子都处于各自的能级时,这一变量值为1。由于只涉及到下面的三个能级,因此n1 + n2 + n3 = 1。(参数 nj 可看做激发密度,单位为m−3;只有在速率方程系统中存在非线性项,例如,对于能量转移过程,方程的形式依赖于这种解释)参数Ajk 代表从能级j到k的自发跃迁速率,单位为s−1。例如,A21 是上能级寿命的倒数。另外,方程中包含吸收和受激辐射速率,它们由跃迁截面(具体数值与波长有关),泵浦光和信号光光强和光子能量同时决定。
多光子跃迁过程 3 → 2在增益介质具有很高的声子能量时通常比较强。因此n3 通常比较小(极高泵浦光强情况下除外),因为离子被泵浦到能级3后会很快转移到能级2上。因此,忽略掉3能级上的粒子数是合理的,并且其它的跃迁也从这一能级开始。因此系统方程简化为:

当然其中的一个方程是多余,因为两个能级的布居数和在任何情况下都等于1.
特定情况下会增加复杂性:
通常会加入附加项,例如能量转移过程。在上转换过程中,改项正比于n22 ,其中能级2中的离子将能量转移到同能级的离子中,结果基态和另一个更高的能级分别多了一个离子。假设更高能级的离子很快衰变到能级2中,系统方程的附加项会相对简单。另一个例子,文献中讨论了氟化物光纤中铥离子更加复杂的能级,包含了一些激发态吸收过程。
也可能要包含不同种类离子间的能量转移项。常见的一种情形是掺铒镱光纤中,主要是镱离子吸收泵浦辐射,将能量转移到铒离子上。这一模型于是要包含所有涉及到的离子的能级布居数和相应的耦合项。
如果光纤放大器中存在放大的自发辐射,那么这时涉及到其它的波长。在数值模型中,ASE光谱被分成分立的波长槽,每一个分别对应不同的吸收和辐射截面。
一般来讲,需要在增益介质的不同位置计算速率方程,因为光强同时与纵向和横向坐标有关。
解速率方程以及应用
对于增益介质某指定位置以及指定光强的情况,粒子数密度随时间的变化可以将速率方程对时间积分进行计算。可以采用荣格-库塔方法。但是,速率方程通常被称为刚性系统的微分方程,时间常数非常不同。系统中最快的过程(例如,相对比较快的非辐射跃迁)需要使用小的时间步长,否则数值解是不稳定的。同时,一些更慢的过程需要演化过程需要在一个长的时间域上计算,因此需要许多数值步骤。鉴于此,在给定光强的情况下,单纯的采用模拟时间演化过程来计算稳态布居数密度效率很低。
在简单的情况下,可以简单的分析计算在确定泵浦和信号光强时的稳态粒子数。例如,简化的系统方程可以得到下列结果:

也可以同时计算布居数密度和光功率的变化,例如,为了给出调Q激光动力学模型。那么微分方程组就包含了布居数的速率方程以及光功率的动力学方程。
在许多情况下,得到空间平均粒子数密度是非常方便的。在简单能级的情况下,增益介质中的粒子数由一个简单的变量表示,它与激光器增益直接相关。这一变量可以作为一个动力学变量用于i类子书和激光强度的动力学方程中,参阅词条激光动力学。
速率方程模型的局限
速率方程描述了能级粒子数的统计学变化情况,并且是基于一些假设之上的。它们不能描述相干过程,例如拉比振荡,因为它们是对很多离子取平均值,这些离子处于不同的微观环境中具有不同的光强。并且假设了所有离子方程类似。后面的假设当增益介质中存在团簇时不成立。在这种情况下,团簇中的离子会具有很强的上转换过程,因此在模型中需要被看做单独的种类来计算。这一拓展后的模型已经建好,更加复杂,通常涉及很多参数,很难在实验中得到。