光纤光学中一种很简单的反射装置（反射镜）是制作一个光学环，利用一个2*2定向光纤耦合器，其中一边的两个端口连接在一起（如图1）。 

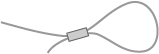
  图1：一个简单的光纤环反射镜。 

如果在其一端口输入光（例如，图1中上面的端口），光被分为两个相反方向的光在环中传播。当这两束光在耦合器中再次结合，它们会相互干涉。干涉效应决定了返回到入射端口和另一个端口出射的功率分配。干涉条件会受多模特性，偏振态变化和非线性效应的影响。 

光纤环反射镜也可以看做是一个Sagnac干涉仪。 

线性的光纤环反射镜 

最简单的情况是只采用单模光纤，并且在传播过程中偏振态不发生改变。（可以采用保偏光纤或者光纤偏振控制器。）并且，假设功率非常低，以至于非线性效应（尤其是克尔效应）可以忽略。另外，假设光纤中没有光强损耗，并且光纤耦合器的功率分离比为50:50（即，3-dB耦合器）。在这种情况下，干涉条件使所有输入的光重新返回到入射端口。这表明此时光纤环反射镜是一个很理想的反射器，工作在很大的波长范围内，并且在任意偏振态的情况。光纤环的长度对结果也没有影响。同样的，光纤环中的环境效应，例如温度改变，不会有影响，因为它不能影响偏振态。 

如果功率分离比偏离50:50，那么不能得到100%的反射率。图2给出了演示。但是，结果仍然与环的长度无关。 

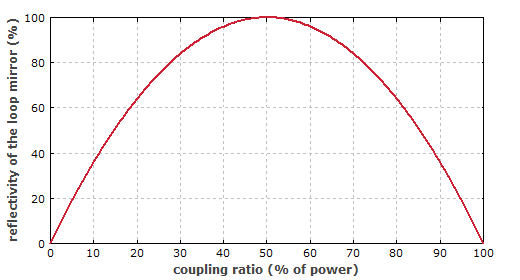
   图2：线性的光纤环反射镜的功率反射率随光纤耦合器耦合比的变化曲线。 

由于光纤耦合器的耦合比与波长有关，因此该曲线可以转化为光纤环反射镜反射率随波长的变化。 

反射率与波长强相关的同时还会受到双折射的影响。如果光纤环采用很高双折射的光纤（例如，一个保偏光纤），并且偏振态由光纤偏振控制器仔细调整，那么得到的光谱透射方程会实现振荡。光谱周期反比于双折射（两偏振方向的折射率差）和光纤长度。由于透射凹陷位置与温度和应力有关，这种装置可用于光纤传感器中。其优势在于，当测量双折射随干涉的变化时，无需考虑环境因素对双折射光纤与普通光纤连接处的影响。也可以实现与温度无关的应力传感器，这时需要采用高双折射的光子晶体光纤，其双折射与温度几乎无关，至少当聚合物涂层去除后与温度几乎无关。 

非线性光纤环反射镜 

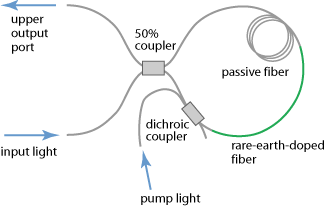
  图3：非线性放大环反射镜，包含一根有源光纤和一根更长的无源光纤。

光纤中传播超短脉冲时，非线性克尔效应非常强，因为峰值功率很高。但是，只要光纤环是对称的，并且耦合比为50:50，那么产生的非线性相移就不会影响光纤环的反射率。这是因为在两个方向传播的光的相移相等，因此附加相移不会影响干涉效应。 

在非对称结构中并非如此。例如，光纤环中包含一根稀土掺杂光纤，当输入合适的泵浦光时可以使光放大，还有一根长的无源光纤（如图3）。这种结构成为非线性放大环反射镜（NALM）。当光从左侧以较低功率进入耦合器后，其大部分光被反射到相同的入射端口。而入射具有很高峰值功率的超短脉冲时，环中会产生很大的非线性相位变化。在逆时针方向的相位变化更大，因为该光先经过放大后再在无源光纤中传播。而反方向的波则是在很长的距离上以较低的功率传播。因此，入射光随功率变化的部分进入输出端口时干涉受到影响。 

这一功率相关性仅仅来自于一段无源光纤中的强光学衰减，或者来自于非对称的耦合比。这种情况下得到非线性环反射镜（NOLM）。 

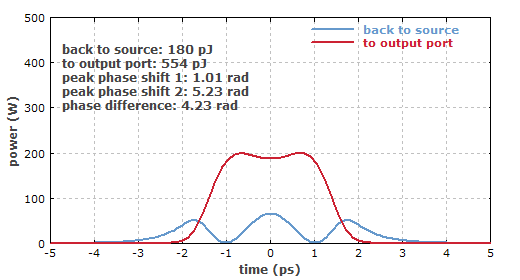
   图4：放大光纤环反射镜时间域上量端口的输出功率曲线。 

其工作细节比较复杂，因为在脉冲时间曲线上非线性相移并不是一个常数，而是在峰值处最大，两侧较小。因此，只能采用数值模拟模型来得到总体性质。图4给出了一个例子，其中环包含1 m长的掺镱光纤和10 m无源光纤。入射脉冲为孤子型的，能量为0.1 nJ，长度为2 ps，很大一部分的输出功率进入上面的输出端口。放大器泵浦光为100 mW，975 nm的光，稳态脉冲列的重复速率为10 MHz。两根光纤都具有正常色散，反常色散区域存在孤子效应，这时非线性环反射镜的性质就有很大的不同。 

在脉冲峰值处，两传播方向上非线性相移的差值大于π，该值是将光耦合进上面的输出端口的理想值。但是，这会增大两侧的耦合。总体来说，这种情况接近于峰值耦合的情况。 

一般来说，脉冲畸变很大，尽管其类型和大小与色散和工作功率等细节密切相关。 

图5给出了上面端口输出能量与下面端口输入能量的比值随入射脉冲能量的变化曲线。它们的相干性受很多效应的影响：放大光纤中增益饱和增大，提高脉冲能量会由于色散和光纤非线性而增大脉冲畸变。 

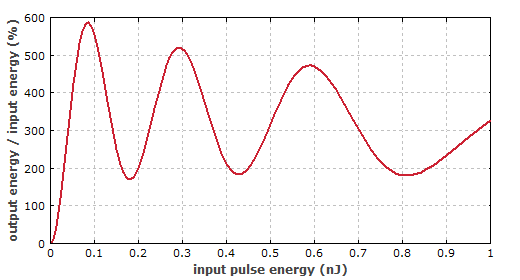
    图5：上端口输出功率的比例随入射脉冲能量的变化曲线。 

非线性环反射镜的应用包括： 

在锁模光纤激光器中，这种装置可作为饱和吸收器，触发和稳定模式锁定，即脉冲形成。一个常见的方案是8字形光纤激光器，其中非线性光纤环反射镜作为8字的一部分，另一部分为一个激光器谐振腔。参阅词条锁模光纤激光器中得到更多细节。 

在光纤通信中，光纤环反射镜可以用作非线性滤波器。例如，某一滤波器可以很好的透射孤子脉冲（无显著畸变），但是会强烈抑制低强度北京辐射，这称为孤子滤波器。在其它需要光信号处理的应用中也很重要。