数值孔径（NA）具有两种不同的含义，分别用于光纤光学和成像光纤中。 

光纤或波导的数值孔径 

在射线图中，光束可以看做在空气中传播，然后入射到具有很大模式面积的阶梯折射率光纤的纤芯上（垂直切割）。 

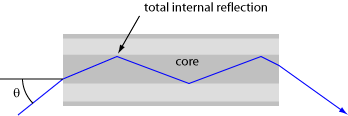
图1：入射光线先经过散射，然后在纤芯-包层界面处发生全反射。只有当入射角不是很大的时候才会发生。 

光纤的数值孔径（NA）是最大入射角的正弦值，这样透射的光束可以在纤芯中传播。NA由纤芯和包层之间的折射率差值来决定，更准确的说可由下列关系确定： 

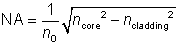
该式是由透射光束以全反射角在纤芯-包层界面传播得到的。其中，n0为光纤附近介质的折射率，如果是空气，那么它约等于1. 

类似的，也可以定义其它波导的NA。 

数值孔径决定的传播角度可以转化为最大的光波横向空间频率，等于数值孔径除以真空波长。（而对于角频率或者横向波矢成分，最大值等于该值的2π倍。）在单模光纤和少量模式光纤中，需要将波传播的细节考虑在内，以上关系只能给出近似的结果，而多模光纤情况下结果是相对准确的。 

在纤芯面积很小时（例如单模光纤），光束的波动特性变得明显，射线图就不准确了。（不能忽略光束发散角。）仍然可以采用上面的式子定义NA。当折射率形状不是矩形时，即非阶梯折射率光纤，该概念就出现问题了。 

大的数值孔径通常对应于光纤末端的基模的光束发散角很大，但是光束发散角也依赖于纤芯直径。对于非阶跃折射率光纤（纤芯的折射率不是常数），可以根据等效阶跃折射率截面定义有效数值孔径，可以得到类似的模式性质。还可以根据纤芯最大处的折射率计算数值孔径。还有其他基于光纤出射光的远场形状的方法，通常取光强衰减到最大值的5%时角度的正弦值。在任何情况下，采用数值孔径值时需要指出其具体的定义，因为不同的定义会得到不同的结果。 

单模光纤的NA通常在0.1量级，但是可以在0.05-0.4之间变化。多模光纤通常具有更大的数值孔径，例如0.3。光子晶体光纤的数值孔径非常大。 

大的数值孔径可以得到： 

• 给定模式面积，数值孔径越大，导波效应越强，能支持更多的模式数目。 

• 单模导波需要更小的纤芯直径。对应的模式面积更小，因此光纤末端光束的发散角更大。光纤非线性相应的会增加。相反的，大模式面积单模光纤的数值孔径很小。 

• 弯曲损耗减小；光纤可以更大的程度的弯曲。 

• 随机折射率涨落对导波的影响变小。（对于大模式面积低数值孔径的单模光纤，这是一个很大的问题。） 

• 纤芯掺杂浓度越高，需要的折射率差越大，因此会提高散射损耗。纤芯-包层界面的不规则性也会带来相同效应，这在折射率差很大时非常重要。 

透镜的数值孔径 

透镜的数值孔径（显微镜物镜，是透镜的组合）的定义是来自焦点的边缘光纤角度的正弦值与介质折射率的乘积。透镜的数值孔径会限制得到的束腰的尺寸。因此，在数据存储介质（例如CDs，DVDs，蓝光光盘）的播放器和录音机等需要打数值孔径的透镜。 

显微镜中，数值孔径会限制成像的分辨率。可以在样品和物镜透镜之间采用一些具有很大折射率的浸镜油提高数值孔径，这样数值孔径大于1. 

具有大数值孔径的透镜在准直从小孔径得到的激光光束中会用到。例如，低功率单模激光二极管就是这种情形。但透镜的数值孔径如果太小，得到的准直光束会存在畸变甚至被截断。