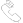光纤和其它波导中的模式的横向形状比较复杂，因此模场面积没有明确的定义。例如，对于高斯光束，直接用光强为最大光强的1/e2的位置所包围的区域来表征模式面积是不合理的。常用的有效模式面积的定义为： 

其中E为电场振幅，I为光强。对于光束半径为w的高斯光束，其有效模式面积为πw2（见图1），通过该公式还可以计算得到其有效模式半径。该公式对于形状为矩形（平顶）半径为w的强度分布也适用。 

                   图1

图1：具有相同有效模式面积的高斯模式和矩形（平顶）模式

图1给出了具有相同有效模式面积的高斯模式和矩形分布模式。在相同光功率的情况下，高斯模式的峰值强度是矩形的两倍。 

对于光纤中的高阶模式，与具有相同有效模式面积的矩形分布模式相比，高阶模式的峰值光强要强很多（如图2）。 

图2

图2：光纤中的LP03模（高阶模）和与其有效模场面积相等的矩形分布模式

利用有效模式面积和非线性系数n2可以计算得到由于克尔效应引起的非线性相移： 

其中P为光功率，L为介质长度。该公式中假设了非线性系数在介质中都是一致的，但是实际上那些使得折射率提高的掺杂物质还会影响介质的非线性。需要注意的是，非线性相移是对整个模式区域而言的，而不是只针对光强最强的地方，这是因为由于波导效应会抑制横截面上的任何大的相位变化。 

根据模式的形状，半径为w的模式，不管是采用1/e2强度值或者D4σ方法得到的有效面积都与 π w2差别很大。大多数实际情形中，差值不是特别大。 

典型的用于光纤通信的单模光纤的有效模式面积在100μm2左右，而大模场面积光纤的有效模场面积则会大好几倍（有些会大于1000um2）。而有些光子晶体光纤的有效模式面积则会小于10um2。 

对于小模式面积的光纤，一个很重要的特性就是在相同的光功率下，光强会大很多，因此非线性效应也就会很显著。此外，小的模式面积通常是由较强的波导效应导致的，因此其弯折损耗会较小，而且受外界的干扰也会较小。 

在词条模式半径中有一个方程可以计算阶跃折射率光纤的模式半径（及有效模式面积）。 

将两个有效模式面积不同的光纤熔接一起时，会产生一定的损耗。词条光纤接头中有一个方程可以估计耦合损耗。为了实现低损耗（即高效率）的光纤连接，需要使用模式大小转换器（或模场面积适配器）。通常它是由锥形光纤制作的，可以扩展或者压缩光纤的模式。